Introduction
In this post, i will walk through the logic and implementation of Kruskal’s algorithm for finding Minimum Spanning Trees. In case if you don’t know about Minimum Spanning Trees, this post will give you a quick start.
Kruskal’s alogrithm tries to form a forest of trees and tries to connect them using edges with minimum weight resulting in Minimum Spanning Tree. Let’s try to look into its working using example.
Logic of Kruskal’s Algorithm
Let’s consider a graph given below
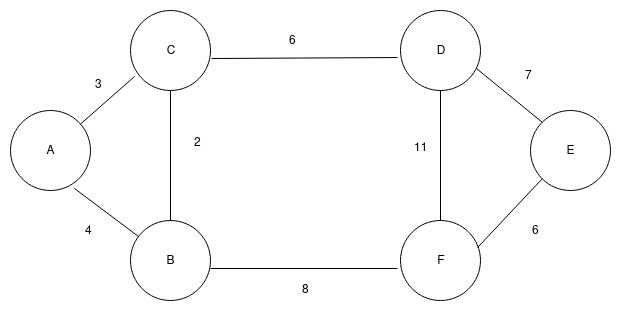
a. Let’s take edge with minimum weight as our initial tree which is (B,C) with weight 2. I use different yellow edge for showing edges currently in MST. Thus our graph would look like,
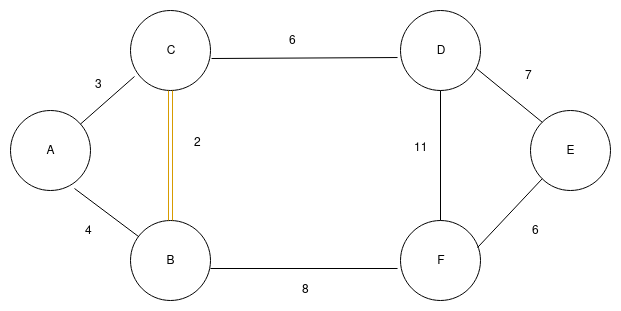
b. The next edge with minimum weight is (A,C) with weight 3.Since these sides our not connected in any tree in our forest. We will add this edge in MST making our graph look like,
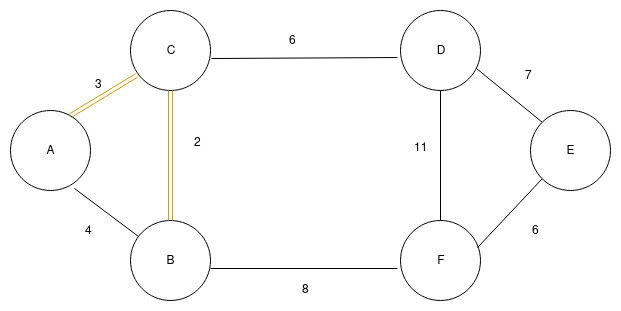
c. Next edge is (A,B) with weight 2 but A is already connected to B via C. In other words, A and C are member of same tree. Hence, we do not need this edge. The next edge is (C,D) and (F,E) of equal weight 6. I am taking (F,E) but it does not matter. So now, we have two tree, one with vertice B-C-A and another one with vertices E-F.
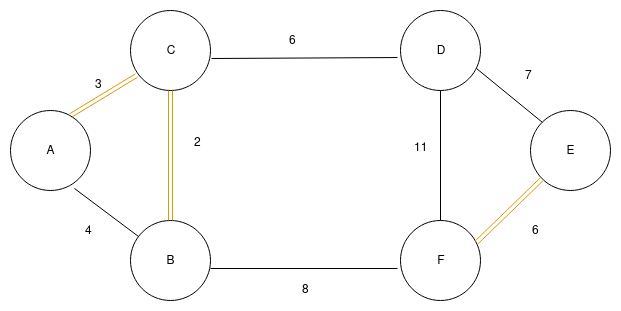
d. The next edge is (C,D) with weight 6. Since, D is not a part of any tree. Let’s add this edge in MST which make it look like,
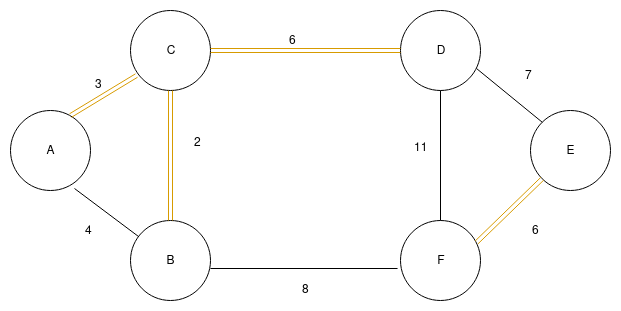
e. Edge with minimum weight which is not in our MST is (D,E) with weight 7. Again, D and E are not connected with each other in our MST. Our graph will be like,
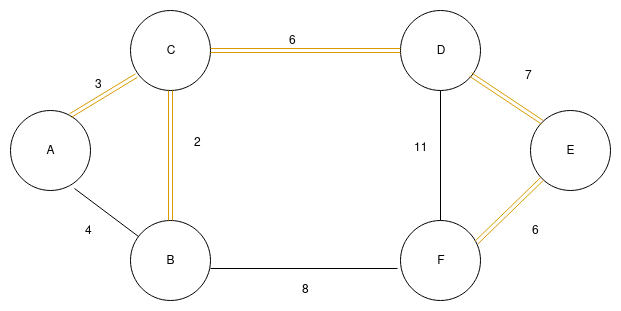
Now, our graph is actually accessible from one node to any other node in MST. If we ignore the sides we have not included in our MST. Our MST would look like,
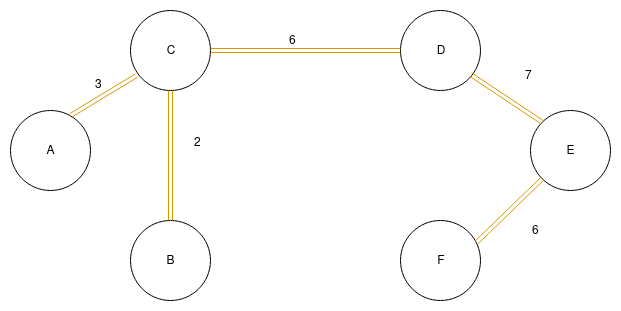
Algorithm
let A be ∅
for each vertex in graph
MAKE_SET(v)
sort all edges of graph in increasing order
for every edge connecting vertices(u,v)
check if FIND_SET(u)!=FIND_SET(v)
then add that edge to A
UNION(u,v)
return A
We are making sets and then sorting our edges in increasing order, The condition FIND_SET(u)!=FIND_SET(v) actually checks if u and v have same parents which essentially means that u and v are already connected with each other. If they are not connected with each other, add that edge to A(MST) and join (u,v) to tree.
Implementation
I use C++ for implementing the Kruskal’s algorithm. You can do it in your preferred language. I create class for graph as well as sets which we will be using in our algorithm. It makes our code easy-to-read and modular.
#include<bits/stdc++.h>
using namespace std;
class Edge{
public:
int source;
int destination;
int weight;
};
//will used to create graph
class Graph{
public:
int v;//number of vertices
int e;//no of edges
Edge* ed;//will store all the edges
void addEdge(int pos,int s,int d,int w);
Graph(int x,int y);
};
Graph::Graph(int x,int y){
v=x;
e=y;
ed=new Edge[e];
}
void Graph::addEdge(int pos,int s,int d,int w){
ed[pos].source=s;
ed[pos].destination=d;
ed[pos].weight=w;
}
//create set
class sets{
public:
int p;//parent
int rank;
};
class subsets{
public:
int v;
sets* s;
subsets(int i);
int Find_Set(int i);
void Union(int a,int b);
void MAKE_SET();
};
subsets::subsets(int i){
v=i;
s=new sets[v];
// we are calling MAKE_SET within constructor
MAKE_SET();
}
int subsets::Find_Set(int i){
if(s[i].p!=i){
s[i].p=Find_Set(s[i].p);
}
return s[i].p;
}
void subsets::Union(int a,int b){
int x=Find_Set(a);
int y=Find_Set(b);
if(s[x].rank>s[y].rank)
s[y].p=x;
else if(s[x].rank<s[y].rank)
s[x].p=y;
else{
s[y].p=x;
s[y].rank++;
}
}
void subsets::MAKE_SET(){
for(int j=0;j<v;j++){
s[j].p=j;
s[j].rank=0;
}
}
int myComp(const void* a, const void* b)
{
//comparator function to use while sorting edges
Edge* a1 = (Edge*)a;
Edge* b1 = (Edge*)b;
return a1->weight > b1->weight;
}
void Kruskal(Graph* graph){
//initialisation
int v=graph->v;
Edge a[v];//will store minimum spanning tree
subsets *s=new subsets(v);
int i=0;//counter for sorted edges
int e=0;//counter for result (a)
//sorting the edges in increasing order
qsort(graph->ed, graph->e, sizeof(graph->ed[0]),myComp);
//main logic
while(e<v-1 && i<graph->e){
Edge next_edge=graph->ed[i++];
int x=s->Find_Set(next_edge.source);
int y=s->Find_Set(next_edge.destination);
if(x!=y){
a[e++]=next_edge;
s->Union(x,y);
}
}
//printing MST
cout << "Following are the edges in the constructed "
"MST\n";
int minimumCost = 0;
for (i = 0; i < e; ++i)
{
cout << a[i].source << " -- " << a[i].destination
<< " == " << a[i].weight << endl;
minimumCost = minimumCost + a[i].weight;
}
// return;
cout << "Minimum Cost Spanning Tree: " << minimumCost
<< endl;
}
int main()
{
int V = 6; // Number of vertices in graph
int E = 8; // Number of edges in graph
Graph* graph=new Graph(V, E);
//A-B
graph->addEdge(0,0,1,4);
//A-C
graph->addEdge(1,0,2,3);
//B-C
graph->addEdge(2,1,2,2);
//C-D
graph->addEdge(3,2,3,6);
//B-F
graph->addEdge(4,1,4,8);
//D-F
graph->addEdge(5,3,4,11);
//D-E
graph->addEdge(6,3,5,7);
//E-F
graph->addEdge(7,4,5,6);
Kruskal(graph);
return 0;
}
It produces following output:-
Following are the edges in the constructed MST
1 -- 2 == 2
0 -- 2 == 3
2 -- 3 == 6
4 -- 5 == 6
3 -- 5 == 7
Minimum Cost Spanning Tree: 24
Time Complexity of Kruskal’s Algorithm
a. The sorting operation takes ElogE time.
b. While loop containing UNION and FIND_SET operations on takes disjoint sets takes O(E) time and MAKE_SET takes O(V) time. Total time taken by both loop is O((V+E)α(V)) where α(V) is very slowly growing function because running time for union by-rank is O(mα(n)), that is, m disjoint-set operation on n elemenets.
c. Since graph is connected, |E|>=|V|-1, so disjoint operations take O(Eα(V)).
Thus, total running time for kruskal’s algorithm in O(ElogE).Since |E|<|V|^2, thus lg(E)=O(lg(V)). Thus, running time of kruskal’s algorithm is O(ElogV).