Minimum Spanning Tree

Introduction

Suppose we have n cities and there are m paths(or highways) interconnecting them. Now we know that n cities can be connected using n-1 paths and we also wish to use paths with minimum possible distance between them.

Now, we can model the same problem using graphs of v vertices and e edges.let T be a acyclic subset of e such that it connects vertices and total weight of all edges is minimum. This T is what we call a “Minimum Spanning Tree”. T is called Tree not graph as it do not have any cyclic component, thus, T is of the form of a tree.

How to generate MSP

We need to find a edge of minimum weight connecting two parts(which can be two edges too) of a graph.Thus we need to find edge with minimum weight which is also called light edge.

Consider a graph as shown below,

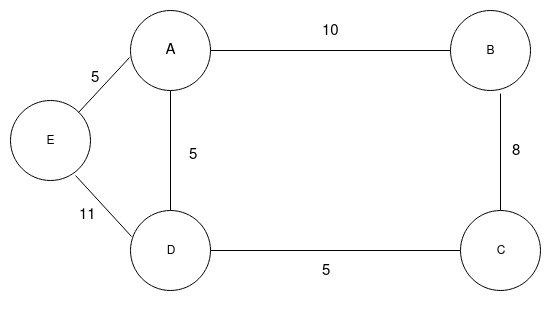
The graphs consist of five vertices which are connected with a number of edges. Now, Suppose we draw a imaginary cut on the graph which separates it into two parts.

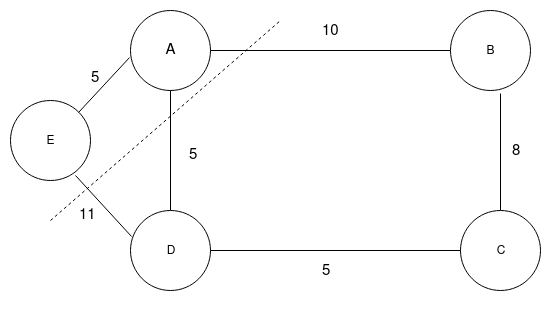
There are 3 edges which connect A and E vertice to rest of the graph of weight 11,5 and 10. Since edge joining A and D of weight 5 is minimum, we can use this vertice to connect both parts of network. We can also say that edge AD is light edge.

At this stage we can form a general algorithm to develop a minimum spanning tree.

let A be ∅ 
while A does not form a spanning tree
    do find a minimum edge (u,v) which is safe for A
       add this edge to A
return A 

Algorithms used to generate MSP

Logically, there are two ways to generate MSP

1. Think graph as a forest of trees(which only have root nodes at the beginning) and try to check if there’s a link between two forest. If there is multiple links choose one with minimum weight. This method is also known as “Kruskal’s algorithm”.

2. Another way could be used to select a node first and check its connecting node and connect it with neighbouring node of least weight and move to that node and keep doing it until you connect all nodes of trees. This method is called “Prim’s algorithm”.