Prim's algorithm

Introduction

Prim’s algorithm is used to find Minimum Spanning Tree along with Kruskal’s algorithm.In case you want to learn about Minimum Spanning Tree, this post will give you a quick start.

Prim’s algorithm starts from any arbitrary node and continue to expand by including edges having minimum weight until all edges are included in Minimum Spanning Tree.

Logic of Prim’s Algorithm

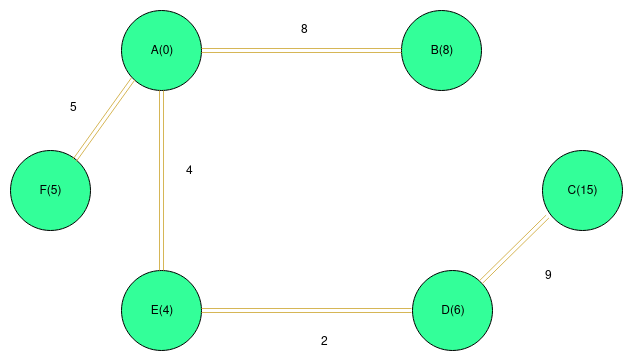
Consider a graph as follows:-

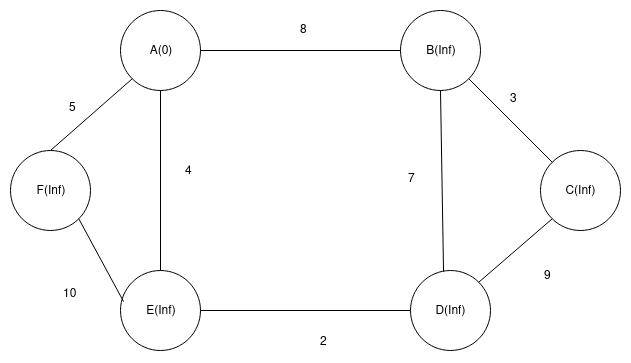
Here values inside() represent key value of that vertice which is Inf(infinity) initially.Since we will start with vertice A, we set its key value as 0.

1)Update key value of all adjacent vertice of A and select next vertice having minimum key value in graph which is E.

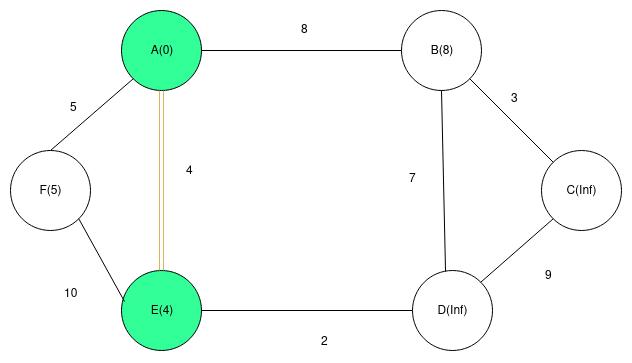
2)Update key values of all the adjacent vertex of E and select the vertex with minimum key value, which is F.

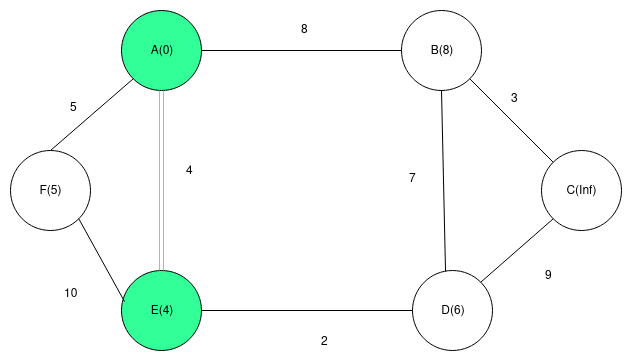
3)Since all the vertice adjacent to vertex F are already included in MST. We will add it to MST and look for next vertex with minimum key value which is D. Update key values of all vertex adjacent to D(which is C). Our graph would look like,

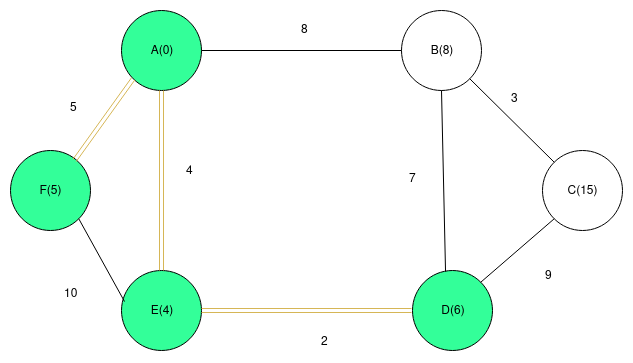
4)After repeating the same step as above, out MST would look like

Algorithm

In this algorithm, key[v] represents minimum distance(or weight) of all the edges connecting v with neighbouring vertices while pi[v] represents parent of vertice v in Minimum Spanning Tree. We are using Minimum priority Queue with key[v] to get unvisited vertice with minimum weight.

Prim(r)

1	for every vertex v in Graph
2		do key[v]=∞
3		   pi[v]=NIL
4	key[r]=0
5	Insert all vertices in min-priority Queue Q
6	while Q≠∅
7		do u=EXTRACT_MIN(Q)
8		   for each vertex in adj[u]
9		       do if v∈Q and w(u,v)<key[v]
10		          then key[v]=w(u,v)
11		               pi[v]=u

Implementation

As mentioned earlier, We are using Priority Queue to find unvisited vertice with minimum weight but we can also do the same using a boolean isVisited and loop through all unvisited nodes while looking for minimum weight. This method is inefficient but is easy to implement than priority Queue.

#include<bits/stdc++.h>
using namespace std;

# define INF 0x3f3f3f3f
#define NIL -2

class Graph{
    int v;
    list<pair<int,int>> *adj;
    int minKey(int key[],bool isVisited[]);
    void printMST(int pi[],int key[]);
public:
    Graph(int vertices);
    void addEdge(int src,int dest,int weight);
    void Prim(int r);
};

Graph::Graph(int vertices){
    v=vertices;
    adj=new list<pair<int,int>>[v];
}

void Graph::printMST(int pi[],int key[]){
    cout<<"Edge \tWeight\n";  
    for (int i = 1; i < v; i++)  
        cout<<pi[i]<<" - "<<i<<" \t"<<key[i]<<" \n";
}

void Graph::addEdge(int src,int dest,int weight){
    adj[src].push_back(make_pair(dest,weight));
    adj[dest].push_back(make_pair(src,weight));
}

int Graph::minKey(int key[],bool isVisited[]){
    int min=INF,min_ver=NIL;
    for(int i=0;i<v;i++){
        if(isVisited[i]==false && key[i]<min){
            min=key[i];
            min_ver=i;
        }
    }
    return min_ver;
}

void Graph::Prim(int r){
    int key[v];//store the key of vertice v
    int pi[v];//store the parent of vertice v
    bool isVisited[v];

    for(int i=0;i<v;i++){
        key[i]=INF;
        pi[i]=NIL;
        isVisited[i]=false;
    }

    key[r]=0;//taking 0 as source
    pi[r]=NIL;

    for(int i=0;i<v-1;i++){
        //v-1 as v-1 edges are needed to create a MST of v edges
        int u=minKey(key,isVisited);
        list<pair<int,int>>::iterator itr;
        isVisited[u]=true;
        for(itr=adj[u].begin();itr!=adj[u].end();itr++){
            int v=(*itr).first;
            int w=(*itr).second;
            if(pi[v]==NIL && w<key[v]){
                pi[v]=u;
                key[v]=w;
            }
        }
    }
    printMST(pi,key);
}

int main()  
{
    int V = 6; 
    Graph g(V); 

    //  making above shown graph 
    g.addEdge(0, 1, 5); 
    g.addEdge(0, 2, 5); 
    g.addEdge(1, 2, 10); 
    g.addEdge(0, 3, 8); 
    g.addEdge(1, 4, 2); 
    g.addEdge(3, 4, 7); 
    g.addEdge(3, 5, 3); 
    g.addEdge(4, 5, 9); 

    g.Prim(0); 

    return 0;   
}

It produces following result:-

Edge 	Weight
0 - 1 	4 
0 - 2 	5 
0 - 3 	8 
1 - 4 	2 
4 - 5 	9

Time Complexity

lines 1-3 takes O(V) time to complete for a Graph G(V,E). While loop runs for O(V) time while line 7 in our implementation takes O(V) time. lines 8-11 runs for O(E) time. Hence, time complexity will be O(V.E).

But if we use min-priority queue, line 5 will run for O(V) time to create a queue while line 7 will take O(vlogV) time. for loop in lines 8-11 will run O(E) time and operation in line 10 is a Decrease-KEY operation which takes O(logV) time. Thus total time will be O(VlogV+ElogV) which is O(ElogV).Total time would be O(ElogV).

The time complexity can further reduced by implementing priority queue using fibonacci heaps which perform EXTRACT-MIN in O(logV) and DECREASE-KEY in O(1) time. Hence it’s running time becomes O(E+VlogV).